The CacheLib Caching Engine: Design and Experiences at Scale

30 Sep 2022

Link	https://www.usenix.org/system/files/osdi20-berg.pdf
Year	OSDI 2020

This post will focus on the CacheLib paper. A separate post will focus on the engineering design and usage of CacheLib.

The Big Ideas

• The prior assumption that item popoluarity distribution follows a zipf distribution of 0.9 < alpha <= 1 is incorrect. Meta workloads have lower alpha and some do not follow zipf.
  • zipf is a inverse distribution. Larger alpha is easier to cache.
• Meta workloads have a large degree of churn: changes in item popularity. Item popularity drop off after ~1 hour.
• Negative caching: storing keys for entries that definitely do not exist in the database (>50% of social graph requests).
• The 4 main caching uses cases at Meta are: social graph, application lookaside, CDN, and storage, each consisting of ~20% usage.

CacheLib Motivations

CacheLib is a C++ caching library for both building caches and accessing caches. This library provides a set of core caching functionalities and aims to unify the various specialized caches in Meta. From the paper, Meta used to independently develop caches for different subsystems (e.g. CDN, graph, storage). The authors argue that this disjointed approach is suboptimal because it 1) requires large amount of engineering effort to maintain due to redundant code 2) makes sharing optimizations across subsystems difficult. In summary, the key goal is a general-purpose caching library.

However, similar to the generalization-vs-specialization debate, converting from specialized cache to CacheLib cannot be all all sunshine and rainbows. First, not all specialized caches can be converted to using CacheLib. One example the paper provided is ad-serving systems, which rely on caching nested data structures. CacheLib cannot support this as it only supports “data structures that map into a flat address space”.

• I am not exactly sure what this means. Does this mean the data items have to consume contiguous address ranges? E.g. arrays. It is likely that several CacheLib designs and optimizations rely on this restriction.

I recall that one of the main (claimed) advantages of Redis is that it supports caching a wide range of data structures, including nested ones. I do not know how important this support is to Meta’s caches and in-memory caches in general. Perhaps the cients can take care of the nest data structure organization on the client end using CacheLib.

Second, CacheLib cannot always provide competitive performance. The authors provided a case where CacheLib was eventually able to eventually improve the performance of a specialized CDN cache by adding features into CacheLib. While this seems like a success story, the potential underlying problem is that CacheLib may end up having more and more specialized features. By accomodating too many specilized features, other problems may arise (e.g. CacheLib becoming too complex). Perhaps there needs to be a balance.

Caching Challenges at Meta

Caching Workloads

The authors present several cache use cases at Meta.

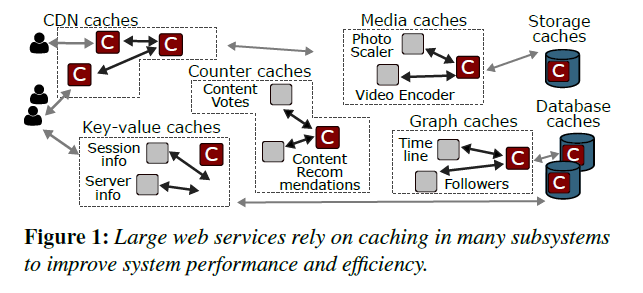
• CDN caches: serves media objects such as photos, audio, and video. These CDN servers are physically located near the user to reduce the latency and network traffic. These caches are remote caches. I am not sure whether the CDN servers are running workloads other than the CDN caches.
• Application lookaside caches: these are general remote caches used by web applications to store e.g. user data. The term “lookaside” typically means that upon a miss, the client is responsible for retriving the missing item from the backend store and potentially inserting this entry into the cache. The paper does not explicitly mention whether this is true or not. Perhaps this is common for distributed in-memory caches.
• In-process caches: the cache instances runs on the same server as the client application, improving both latency and bandwidth (although cache misses should still require remote access). The tradeoff here is the extra resource consumed by the cache. The cache can therefore content resources from the client application and even cause OOM.
• ML caches: the authors list two ML use cases, input caching and output caching. Input caching is caching ML model inputs (e.g. how many likes to sports related pages). This is interesting, since it implies that some parts of the ML runs on the client side. Of course, “client” here does not nessesarily mean the user’s device. I imagine this could be e.g. the deep learning recommendation model (DLRM) services. Output caching is caching the ML model outputs, in case there are model predictions that have the same inputs. Here, the client could potentially be the user’s device.
• Storage-backend caches: Meta uses flash drives as caches of spinning disks. Do these caches still use DRAM, or only the flash?
• Database page buffer: this sounds to me is caches sitting in front of databases. Perhaps the difference between this type of cache and lookaside caches is that each database page buffer cache is dedicated to a particular database, whereas each lookaside cache correspond to an applcation.

So it seems that there are multiple levels of cache even when considering only one application and the data center stack it interacts with. E.g. in-process cache within the client to cache latency critical data, remote application lookaside cache, database page buffer cache, and storage-backend cache.

Cache Workload Behaviors

This is the profiling part of the paper, which in itself is already valuable.

Here the authors study 4 cache workloads: Lookaside, SocialGraph, Storage, CDN. Both Lookaside and SocialGraph are application lookaside caches, while SocialGraph is used specifically for caching social graph information.

Large Working Sets

Here, the term “working set” refers to the set of data that are considered popular (although how popular is not defined). The authors analyze the popularity distribution and churn rates.

Poularity distribution is shown on Figure 3. Ideally, we would want these plots to have a very steep negative slope, meaning that a small amount of data is extremely hot, making caching easy.

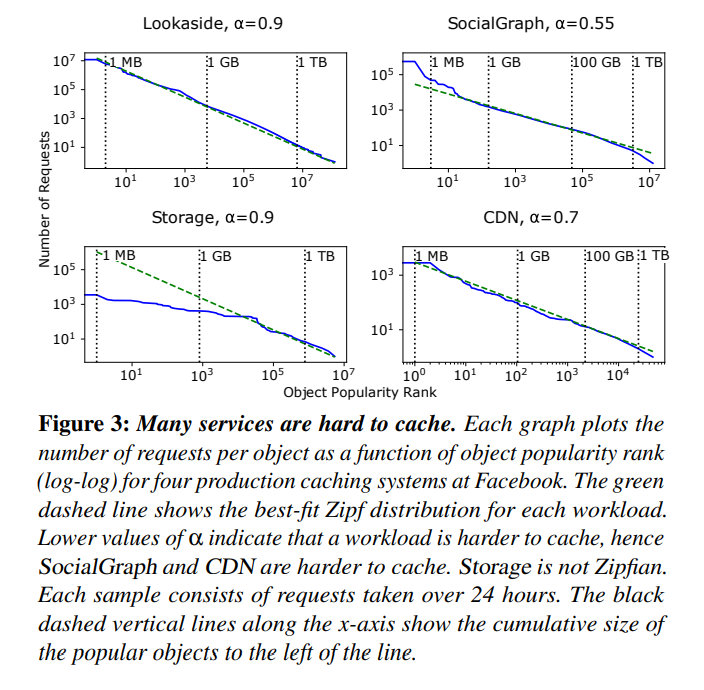
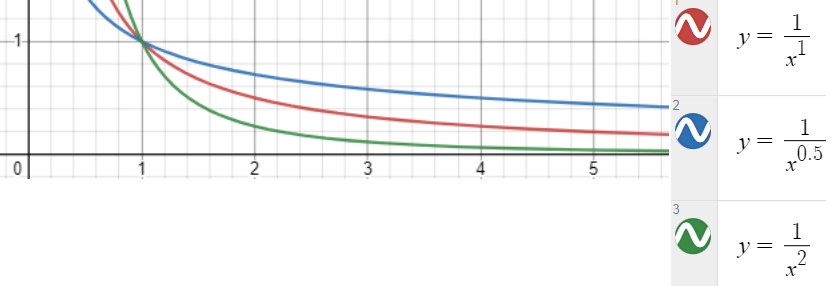
The formal definition of a Zipf distribution is that the i-th most popular object has a relative frequency of 1/i ^a. The most popular object then has a relative frequency of 1, the second most popular 1/2^a. The greater the value of a, the faster the decay, meaning a smaller hot set. This paper claims that past profiling/benchmark papers used 0.9 < a <= 1 as the standard evaluation assumption, while SocialGraph and CDN shows smaller values of a, causing a larger working set.

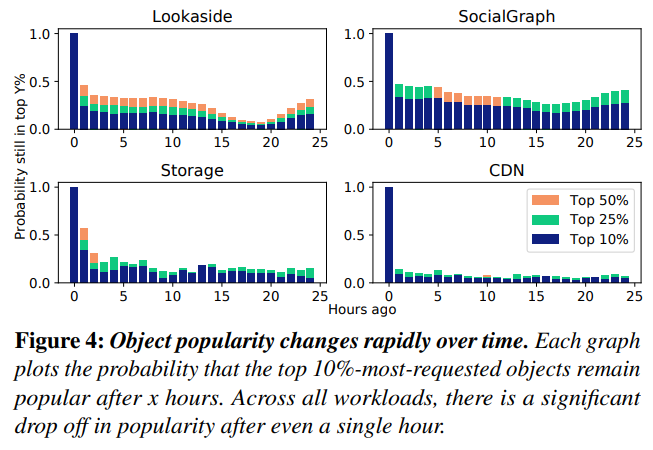
The authors define churn as the change in the working set due to changes in key popularities. Meta workloads show a high degree of churn, as shown in Figure 4. Hot objects typically drop off in popularity after an hour. The popular YCSB assumes there is no churn, meaning that each key will have the same popularity throughout the benchmark. However, it is unclear whether this no-churn assumption makes a big difference. If the churn varies smoothy during the 1 hour, perhaps it does not impact the overall performance significantly. More evaluation is needed.

While the topic of this section is “massive working set size”, the authors in fact do not provide actual working set sizes, but instead show indirect evidences such as the popularity distribution. The vertical dashed lines in Figure 3 give some hints. It is also unclear what is the effect of TTL on the working set size. The recent work from Twitter [1] observes that TTL effectively bounds the working set size (see Figure 7).

Size Variability

I am assuming the object size here refers to the value size. The key size should be relatively small compared to the values. Figure 5 shows that the two application lookaside caches, Lookaside and SocialGraph, have many small objects < 1KB. This makes sense since they are used to cache general application data such as user data and social graph nodes. One implication is that caches should have small per-object memory overhead if it aims to store small objects in the order of 10s of bytes.

CDN only has objects larger than 100B and ~60% of the objects are 64KB large. Storage only has 128KB objects. This is because CDN and Storage split large objects into 64KB and 128KB chunks respectively.

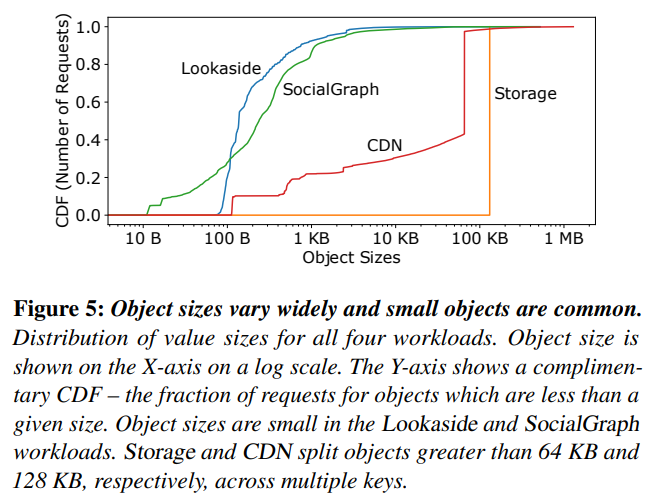
In YCSB, the size variability can be configured (in a somewhat coarse grain manner) using fieldlengthdistribution, which can be one of constant, uniform, or zipfian [2]. Of course, YCSB also supports trace replaying (with some amount of engineering).

Negative Caching

Negative caching stores key entries indicating that the requested object (e.g. connections between two users) definitely does not exist. Without it, the client would need to search in both the cache and the backend database to ensure the object does not exist. 55.6% of requests to SocialGraph are for keys that do not exist.

Negative caching is implemented using a DRAM compact cache, which optimizes for storing objects smaller than a cacheline (64B), since a negative cache entry only requires storing the key.

Summary

Workload/Challenge	Popularity distribution	Size variability	Negative caching
Lookaside	alpha = 0.9	100B-1KB	Not used
SocialGraph	alpha = 0.55	10B-1KB	56% of all requests
Storage	not zipf	64KB and less	Not used
CDN	alpha = 0.7	only 128KB	Not used

Evaluation

Emulating Churn (Correctly?)

The authors emulate churn by continuously introduces new keys at a configurable rate. Based on the CacheLib documentation [3], this should be the loneGet operation. Since loneGetRatio is a single value, I am assuming that the amount of churn is constant throughout the benchmark. E.g. 10% of accesses are request for a key that does not exist in the cache. However, I found this to be questionable. Based on this paper’s own definition in Section 3.1, churn is “the change in the working set due to the introduction of new keys and changes in popularity of existing keys over time” (emphasis mine). The proposed methodology only addresses the first half of the definition, but does not seem to change the popularity of existing keys. Since the loneGetRatio is a single constant value, I do not see how CacheBench can emulate a changing popularity distribution simiar to Figure 4. Thus, while the paper correctly point out that YCSB assumes no churn, I do not see how CacheBench supports churn either.

Hit Ratio and Throughput

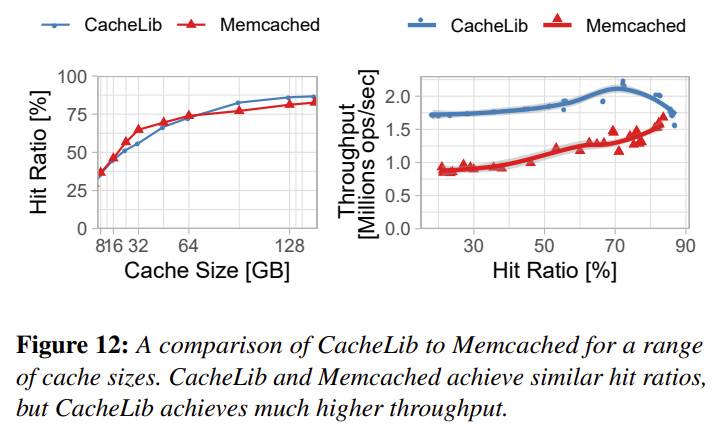
Figure 12 shows hit ratio and throughput comparisons against Memcached. The workload has a working set size of 100 million objects. As the cache size increase, the hit ratio improves as well.

• Interestingly, Memcached has ~10% higher hit rate than CacheLib at cache size = 32GB, which is quite significant. The paper does not explain why this is the case, and I do not have enough understanding to make a hypothesis. More detailed evaluation is required.
• The authors contribute CacheLib’s higher throughput to optimizations that reduce lock contention, such as when accessing LRU list head. The LRU list head stores the most recently used item, so it is stressed when the hit ratio is high. However, at high hit ratios (>80%), Figure 12 shows that CacheLib performs on par with Memcached. In fact, the CacheLib trend in Figure 12 b) shows that CacheLib’s throughput degrades at high hit ratios. I am not sure what the cause is. Need more profiling.
• It is not clear why Memcached cannot implement “optimizations that reduce lock contention”. This does not appear to be a fundamental limitation of Memcached.
• In a realistic caching system, upon a miss, the client would be responsible for fetching the missing data from a backend database, which induces extra latency. However, this extra latency is not emulated in CacheBench (actually, I am not sure if this latency is emulated in any caching benchmark). The source code [4] seems to show that upon a miss, the missing key is immediately inserted into the cache. This results in extra cache throughput pressure that should not occur in a real system. Thus, it is unclear whether CacheLib’s higher throughput at low hit ratios (more misses and cache inserts) is in fact useful.

    // stressByDiscreteDistribution()
    auto it = cache_->find(*key);
    if (it == nullptr) {
      ++stats.getMiss;
      result = OpResultType::kGetMiss;
  
      if (config_.enableLookaside) {
        // allocate and insert on miss
        // upgrade access privledges, (lock_upgrade is not
        // appropriate here)
        slock = {};
        xlock = chainedItemAcquireUniqueLock(*key);
        setKey(pid, stats, key, *(req.sizeBegin), req.ttlSecs,
               req.admFeatureMap);
      }
  

One interesting point is that currently the slab class (I assume they mean allocation class here [7]) tuning (to reduce slab class fragmentation) is done manually. I am not sure what this means yet. I do not see any pararmeters to tune the slab classes in the CacheBench config file [6]. I am also unsure how slab class tuning relates to slab rebalancing [5].

Production Deployment

Interestingly, Meta uses a two-layer hierarchy of caches, with L1 being DRAM-only cache and L2 being DRAM-flash hybrid cache. Only misses in L1 will be forwarded to L2. This provides much larger capacity and thus better hit ratio.

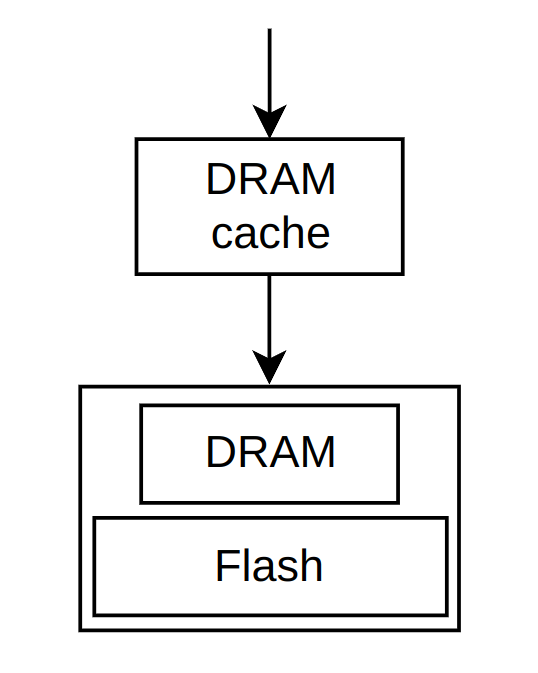
Figure 14 shows the hit ratio distribution for various servers running CacheLib instances. Interestingly, the L1 cache2 has higher hit ratio than the L2 caches. This seems counter-intuitive, since L2 cache has larger capacity than L1. However, only L1 misses will be forwarded to L2. So I am not sure if there is a relationship between miss rate vs. the level of cache. Perhaps they are independent. Even if L1 has 99.99% hit rate, we cannot really tell what the L2 hit rate would be, since it depends on the access pattern of the 0.01% of misses.

Finally, Figure 16 shows the four dominant CacheLib use cases within Meta, which is useful to keep in mind.

Thoughts and Questions

why follow zipf’s inverse distribution? Perhaps more mathematical question.

What role does TTL play? still large working set?

How does TTL effect the large working set size reported? Has TTL been taken into consideration? What is the actual working set size or the caches presented?

Why CacheLib only supports “data structures that map into a flat address space”? What design decisions?

Does CacheBench support churn?

Sources

[1] https://www.usenix.org/system/files/osdi20-yang.pdf

[2] https://github.com/brianfrankcooper/YCSB/issues/587

[3] https://cachelib.org/docs/Cache_Library_User_Guides/Configuring_cachebench_parameters/#operation-ratios

[4] https://github.com/facebook/CacheLib/blob/58161d143ac7b7ab9b8394d637f15bed102f7799/cachelib/cachebench/runner/CacheStressor.h#L340

[5] https://cachelib.org/docs/Cache_Library_Architecture_Guide/slab_rebalancing/#2-how-do-we-pick-a-slab

[6] https://cachelib.org/docs/Cache_Library_User_Guides/Configuring_cachebench_parameters

[7] https://cachelib.org/docs/Cache_Library_Architecture_Guide/overview_a_random_walk#dram-regular-cache