Distributed Consistency and Baseball

24 Jan 2022

This post is my notes while going through the sources. I do not own any of the materials.

Big Ideas

• The consistency requirement depends on the client. Often times, the specific consistency model is fixed by the data set (e.g. bank data needs strong), but baseball shows that it also depends on who is reading the data.
• Clients should be able to choose their own consistency model.
• Review the possible baseball scores example.

give examples on real systems and their consistency models. what are the real world performance implications of each consistency model? What do they mean for real systems?.

Strong and Weak Consistency

The need for consistency arises from replication, which is nowadays almost a first principle in distributed systems: pretty much all large scale distributed systems use replication [source?]. Replication provides both higher fault-tolerance and availablity, but introduces a new problem: consistency. Ideally, we would still like our replicated system to behave as a single machine (strongly consistent).

Weak consistency does not behave the same as a single machine, but often offers better performance. Note that weak consistency is a category of consistency models and not a specific model.

Baseball

Let us first define 6 types of consistencies using key-value store:

1. Strong: get(k) request is guaranteed to return the latest value of k.
2. Eventual: get(k) will return any previously written values of k. No time nor order bound. Weakest model out of the 6.
3. Consistent prefix: the reader observes the correct order of writes, but is not guaranteed how recent the data is. i.e. the reader sees a version of the data that existed at some point in the past.
4. Bounded staleness: get(k) will return a value of k during the last t minutes. i.e. data “freshness” is time bounded.
5. Monotonic reads: while the first get(k) can return any value, subsequent get(k)s by the same client is guaranteed to receive the same or more up to date value. That is, a client will never see an older version of k.
6. Read my writes: if a client write v to k, subsequent reads to k from the same client will return v or a more recent value of x. If not writer, no guarantees and equivalent to eventual.

Visitor and Home are keys. Top table show the writes (increments) to each key in each inning. Bottom table shows all possible results of get(visitor, home). Assume only 1 client is writing. Note that within an inning, visitors bat first.

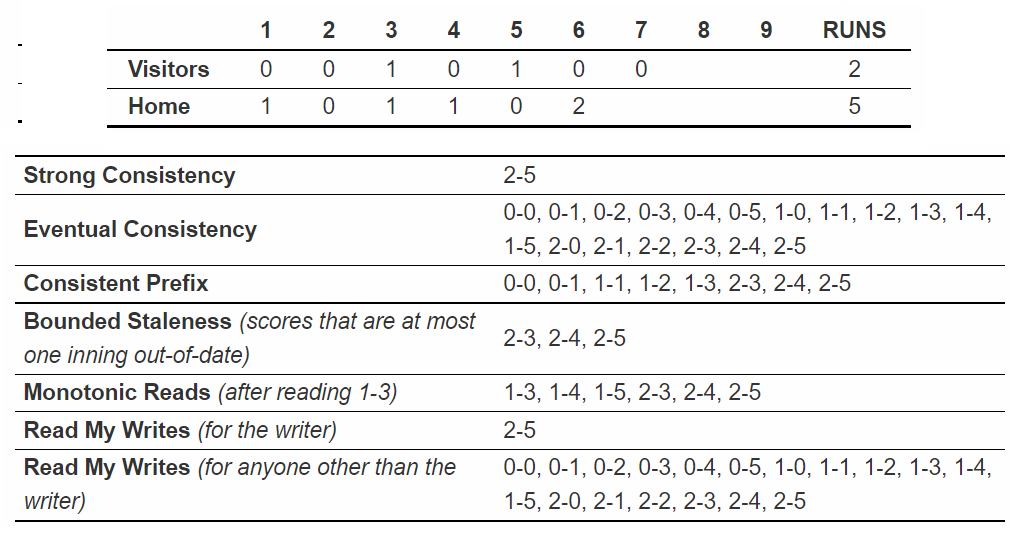
• Strong: only one answer, the latest values
• Eventual: (pretty much) ANYTHING IS POSSIBLE :P Since we can incrementing each key by 1, visitor can take 3 values while home 6, so 3*6=18 combinations possible.
• Prefix: while the data does not need to be recent, the order of writes much be honoured. Thus, we can observe any score that existed in the past. Note that since visitors bat before home in the same inning, 0-2 is not possible.
• Bounded: the scores that occurred during sixth inning.
• Monotonic: note that no order is guaranteed, so 1-4 1-5 possible.
• Read my writes: since only one writer, for a client other than the writer, this is the same as eventual.

Read Requirements for other Participants

Here, each participant is a node with certain assigned tasks. We wish to find what consistencies do each participant require in order to perform their jobs correctly.

Note that each participant may perform read/writes from different server nodes.

• Official score keeper: responsible for maintaining the game score by writting to the two keys.
  • The obvious answer is strong consistency, since the score keeper must be able to read the most up to date scores to do his/her job correctly.
  • Interestingly, can also use read my writes, since the score keeper is the only writer. We use application-specific knowledge to take advantage of a weaker consistency.
• Umpire: we model the role of the umpire as the follows

    if first half of 9th inning complete then
        vScore = Read ("visitors");
        hScore = Read ("home");
        if vScore < hScore
            end game;
  

  • The umpire must have strong consistency. Since the umpire does not write, only strong.

• Radio reporter: ok for score to not be completely up to date. Consistent prefix, since the score must have happened at some point. But that by itself is not sufficient, since we can report 2-5 and later 1-3 (e.g. reading from primary server then a secondary server later). Thus, we need to combine consistent prefix with either bounded staleness (time of one inning) or monotonic reads to constraint the order.

• Sports writer: in this example, the sports writer waits for 1 hour after the game and must receive the correct final score. Thus, bounded staleness of 1 hour.

• Statistician: in this ex, the statistician accumulates the total home team score of the season. To read the score for today’s game, same as sports writer: bounded staleness.
  • To read the accumulated season score, read my writes since is only person writing to it.

Questions

• Replication seems to be a first principle in distributed system in order to provide fault tolerance and high availability. Can we challenge this first principle? Are there alternatives to replication?

Sources

[1] https://mwhittaker.github.io/consistency_in_distributed_systems/1_baseball.html

[2] https://parveensingh.com/cosmosdb-consistency-levels/#consistent-prefix

[3] https://www.microsoft.com/en-us/research/wp-content/uploads/2011/10/ConsistencyAndBaseballReport.pdf