Lamport Clock

26 Oct 2021

This post is my note while studying the sources. I do not own any of the below materials.

Background

Lamport clock is a type of logical clock, which counts the number of events occurred instead of physical time. The goal of a logical clock is to determine the order of events. Why? This is because distributed systems require happened-before relationships in order to function correctly. Why?

In the example below, how can C figure out which message to display first? We could try to attach physical timestamps on the two messages, ie. t1 on m1 and t2 on m2. However, since we cannot get perfect clock synchronization between nodes (ex. if user A’s clock is ahead of user B’s), we could have t2 < t1. gg.

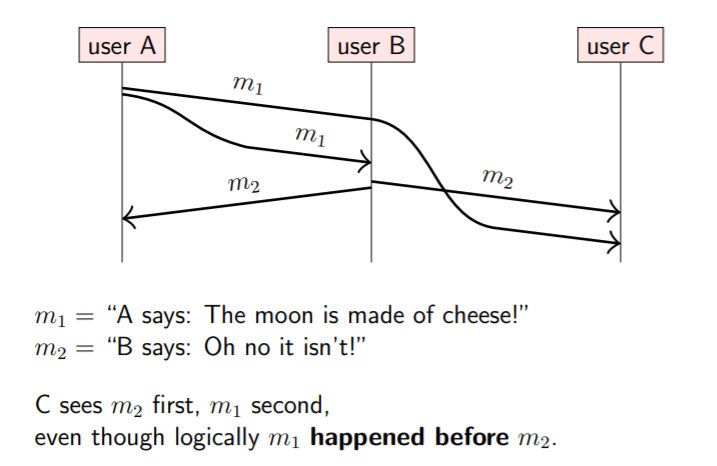
Happens-before

A happens-before relationship is a partial order, meaning that it is possible that for two events a and b, neither a happened before b or b happened before a. In this case, we call a and b concurrent. This is of course not possible in physical time, but we are in logical time here.

More formally…

An event is something that happens at one node. Ex. sending/receiving a message, a local execution step.

Event a happens before event b iff (a -> b):

1. a and b occurred in the same node and an executed before b; OR (note the OR here)
2. event a is the action of sending message m, and event b is the receipt of that message m (can’t receive a message before its sent);
3. there exists an event c such that a -> c, c -> b (transitivity)

Partial order means that it is possible that neither a -> b and b -> a. Then, a || b.

An example set of events are shown below. From rule 1, a -> b; c -> d; e -> f. From rule 2, b -> c, d -> f. From rule 3, a -> c, a -> d, a -> f, b -> d, b -> f, c -> f. a || e, b || e, c || e, d || e

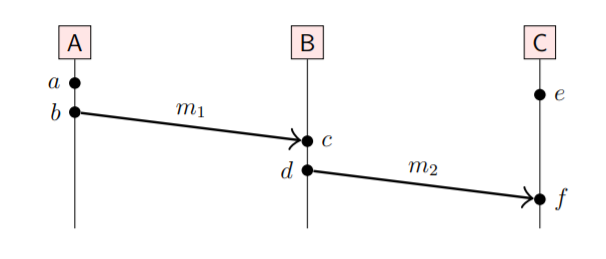
Causality

Again, it’s causal, as in cause, not casual.

The term causality has a similar meaning in physics. Causality describes the influence of one event on another event. For example, if two events a and b occurrs very very close in time (delta t), but are very very far apart (delta d), such that even light cannot reach from a to b ( c < d/t ). In this case, a cannot possibly have affected b, so they are causally unrelated.

In distributed systems, we technically describe the “possible influence” of a on b. We don’t care if a really caused b.

Lamport Clock

Lamport clock is a type of logical clock that describes happens-before relationships between events.

Here is the algorithm in English.

Why don’t we try jumping straight into an example. Based on the algorithm, can you figure out what each timestamp should be?

• The three events in A should be 1, 2, 3 since the counter is incremented on every local event and A does not receive any messages.
• m1 is stamped with 2.
• Since B’s starting counter is 1, as it receives m1, it should increment counter to 3. m2 then is stamped with 4.
• C increments timestamp to 5.

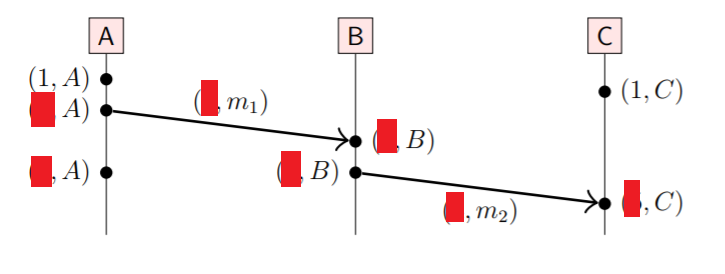
Solution:

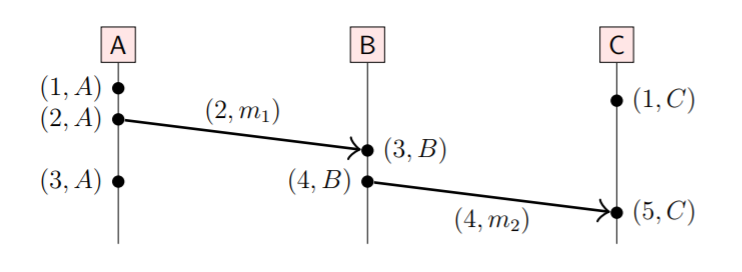
So what happens-before relationships are in this set of events? Let L(a) be the value of t at event a. Some interesting observations:

• (1, A) and (1, C) have the same t, but are concurrent. Does this mean t1 == t2 is not meaningful in Lamport clocking?
• (3, B) has larger t than (1, C), but they are also concurrent. This means that L(a) < L(b) does not imply a -> b.
• But the converse is true, that is, a -> b implies L(a) < L(b). In English, this means that if event a happens-before b, then a’s counter value must be less than b’s.

We can use Lamport clock to extend our partial order (concurrency possible) to a total order by ordering concurrent events lexicographically (aka. alphabetically). In the above example, we then have (1, A) happens-before (1, C).

Sources

[1] https://www.cl.cam.ac.uk/teaching/2122/ConcDisSys/dist-sys-notes.pdf